排序算法¶
Over the years, computer scientists have created many sorting algorithms to organize data.
算法概述¶
算法分类¶
- 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
- 非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
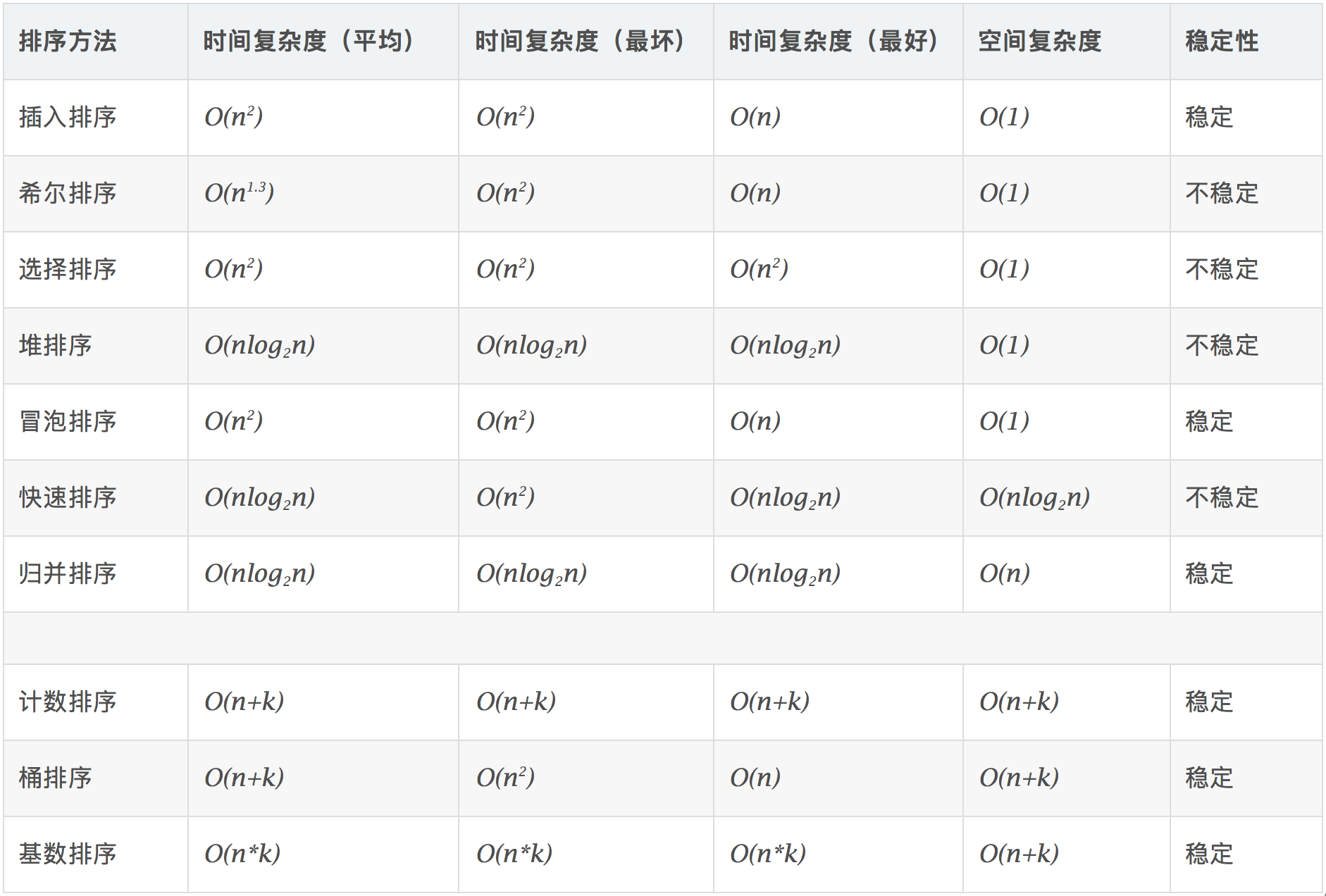
算法复杂度¶
相关概念¶
- 稳定:a=b,如果a原本在b前面,排序之后a仍然在b的前面。
- 不稳定:a=b,如果a原本在b的前面,排序之后 a 可能会出现在 b 的后面。
- 时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
- 空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
冒泡排序 Bubble Sort¶
它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
思想¶
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤1~3,直到排序完成。
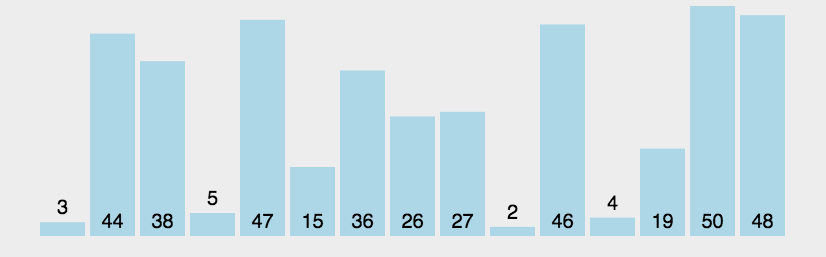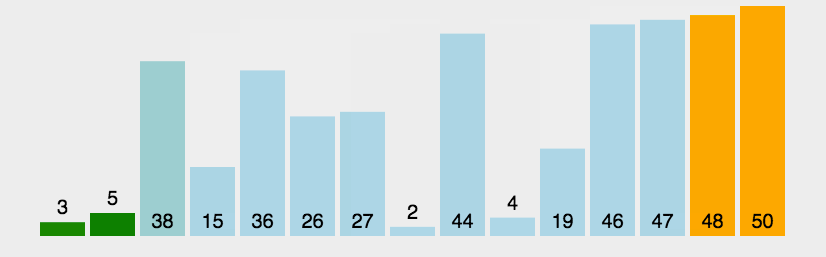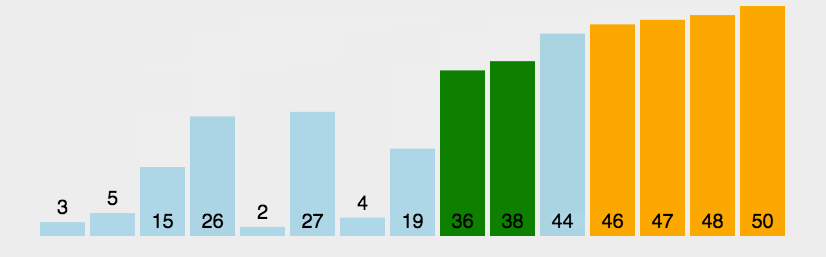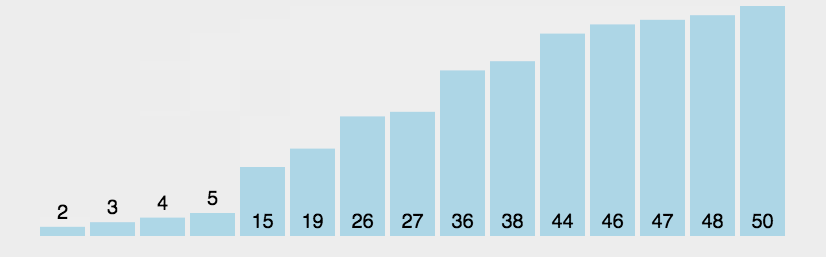
实现¶
def bubble_sort(lst): """冒泡排序""" for i in range(len(lst)): # 遍历数组 for j in range(len(lst)-i-1): # 后i个元素已经排好了 if lst[j] > lst[j+1]: lst[j],lst[j+1] = lst[j+1],lst[j] return lst
优化¶
- 不过,这样做效率非常低。
- 如果只需要在数组中进行一次交换会怎么样?
- 为什么我们仍然要迭代 n ^ 2次,即使它已经排好序了?
- 显然,为了优化算法,我们需要在它完成排序后停止它。
- 我们怎么知道我们已经完成了排序,如果项目是有序的,那么我们就不必交换项目。
- 因此,每当我们交换值时,我们将一个标志设置为
True以重复排序过程。 - 如果没有发生交换,则标志将保持为
False,并且算法将停止。
实现¶
def bubble_sort(nums): # We set swapped to True so the loop looks runs at least once swapped = True while swapped: swapped = False for i in range(len(nums) - 1): # dont have to consider the last i element because we have flag now if nums[i] > nums[i + 1]: # Swap the elements nums[i], nums[i + 1] = nums[i + 1], nums[i] # Set the flag to True so we'll loop again swapped = True
时间复杂度¶
- 在最糟糕的情况下(当列表顺序颠倒时) ,该算法必须交换数组的每一项。
- 每次迭代时,我们的交换标志都会被设置为
True。 - 因此,如果我们的列表中有 n 个元素,那么每个项目将有 n 次迭代
- 因此 bubblesort 的时间复杂度为
O(n ^ 2)。
选择排序 Selection Sort¶
选择排序将列表分为有序列表和无序列表两部分。 不断地删除列表中未排序段中的最小元素,并将其添加到已排序列表中。
思路¶
- 实际上,我们不需要为排序的元素创建一个新的列表,
- 我们要做的是将列表的最左边部分视为已经排序的列表。
- 然后,我们在整个列表中搜索最小的元素,并将其与第一个元素交换。
- 现在我们知道列表的第一个元素已经排序,我们得到剩余项的最小元素,并将其与第二个元素交换。
- 这样一直迭代,直到列表的最后一个项目是要检查的剩余元素。
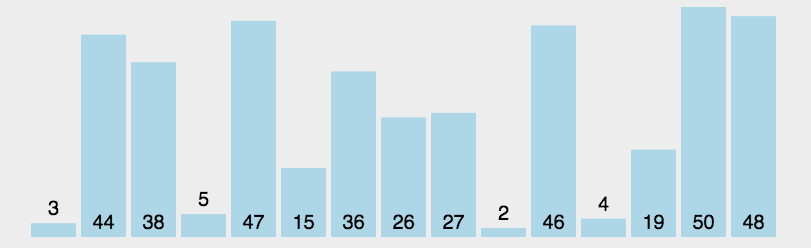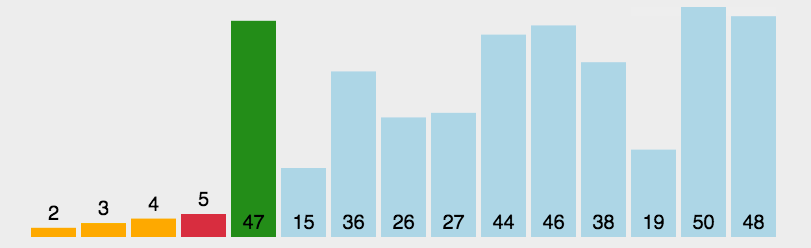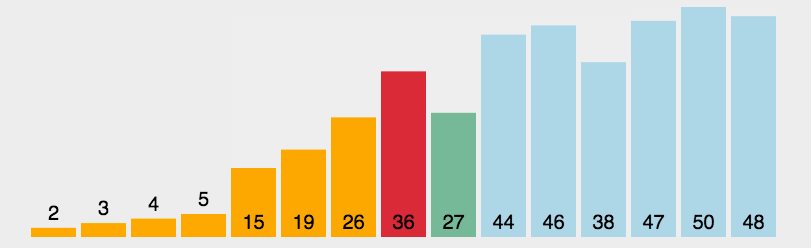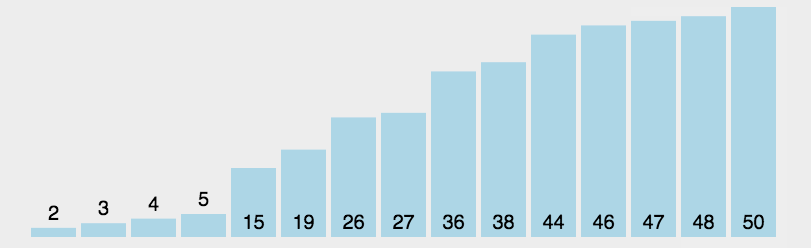
实现¶
def selection_sort(nums): # i表示已经排序好的值 for i in range(len(nums)): # 假设未排序部分的第一个值是该部分的最小值 lowest_value_index = i # 这个循环在未排序部分执行 for j in range(i + 1, len(nums)): if nums[j] < nums[lowest_value_index]: lowest_value_index = j # 将未排序部分中最小的值与未排序的第一个值交换 nums[i], nums[lowest_value_index] = nums[lowest_value_index], nums[i]
时间复杂度¶
- 通过检查选择排序算法中的
for循环,我们可以很容易地得到时间复杂度。 - 对于包含
n个元素的列表,外部循环迭代n次。 - 当
i等于1时内循环迭代n-1,当i等于2时内循环迭代n-2,以此类推。 - 比较的数量为
(n-1) + (n-2) + ... + 1,这使得选择排序的时间复杂度为O(n ^ 2)。
插入排序 Insertion Sort¶
与选择排序一样,这种算法将列表分成有序和无序的部分。 它遍历未排序的段,并将要查看的元素插入到排序列表的正确位置。
思路¶
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置; -重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。
实现¶
def insert_sort(arr): # 第一个数已经排序,从第二位开始 for i in range(1,len(arr)): item_to_insert = arr[i] j = i - 1 # 保留前一个元素索引的引用 # 如果已排序段的所有项目大于要插入的项目,则将它们向前移动 while j >= 0 and arr[j] > item_to_insert: arr[j + 1] = arr[j] j -= 1 # 插入 arr[j + 1] = item_to_insert return arr
时间复杂度¶
- 在最坏的情况下,数组将按相反顺序排序。
- 插入排序函数中的外部
for循环总是迭代n-1次。 - 在最坏的情况下,内部
for循环将交换一次,然后交换两次,以此类推。 - 交换的数量将是
1 + 2 + ... + (n-3) + (n-2) + (n-1),这使得插入排序的时间复杂度为O (n ^ 2)。
堆排序 Heap Sort¶
堆排序将列表分成有序和无序的部分。 它将列表中未排序的段转换为 Heap 数据结构,这样我们就可以有效地确定最大的元素。
思路¶
- 我们首先将列表转换成 Max Heap ——一棵二叉树,其中最大的元素是根节点。
- 然后,我们将该项放在列表的末尾。
- 然后我们重新构建 Max Heap,它现在少了一个值,将新的最大值放在列表的最后一项之前。
- 我们重复这个构建堆的过程,直到删除所有节点。
实现¶
本文主要整理自:
最后更新: 2020-01-21